Exploring the Mathematics of a Safe Practice
As new sailboat owners, my wife Laura and I are mostly fair-weather mariners — a fact I hate to admit in the company of experienced sailors. We have yet to adjust to the often freezing wind chill factor of Pacific Northwest winters and the power of the accompanying storm systems that occur during those months. As a result, Ariel, our Columbia 28, rarely leaves her moorage at our local marina during the winter season.
When we do encounter a day with mild temperatures and excessive breeze, we may venture out onto the Salish Sea; joining the seasoned sailors who are unfazed, or perhaps even beckoned, by heavy weather. On that day, you can bet Ariel’s mainsail will be reefed and her headsail at least partially furled.
Some degree of heeling on a sailboat is desirable, as it comes with increased boatspeed. But once the boat heels too much, speed starts to decrease and control becomes a challenge, which is when reefing is necessary. Reefing the mainsail can provide some balance and control, especially for day-sailers like us and even for experienced sailors like our dockmate, Fred. After nearly 50 years on the water, Fred advises us that, “The time to reef is when you first think about it.”
Before I begin to think of managing Ariel in high winds, I am still learning to trim the sails effectively in light breezes. While I try to get the most out of our old sloop, maximizing speed is not really the goal of our afternoon outings. We’re still at the honeymoon phase of gentle breezes on warm spring days, when we find ourselves harmonizing to the lyrics of Chistopher Cross’ hit song, “Sailing”: “It’s not far down to paradise, at least it’s not for me./ If the wind is right, you can sail away, find tranquility./ Oh the canvas can do miracles, just you wait and see.”
“The canvas can do miracles.” Well, it is kind of miraculous and amazing that a boat can head into the wind and be driven, or lifted, forward like a vertical wing (although I know that Cross was referring to the miracle of what sailing does for our peace of mind). But because of various realities of physics, that driving force also produces a heeling effect in strong breezes.
It’s always alarming and unnerving to hear objects falling from their stowed location in the cockpit or cabin as the wind unexpectedly jumps up a few knots. Even if we were to anticipate the shifting gravity of a hard heel for cabin items, and either anchor them in place or remove them altogether, we’d still have to brace our bodies as they heavily lean toward the drowning toe rail — a situation that is uncomfortable for passenger and vessel alike.
So while we have yet to reef the main mostly because we are, dare I say, a little too chicken to take Ariel out in foul weather, we have tried to understand it and received instructions on the method from experienced sailors. And my takeaway is curious.
The whole process almost seems like cheating, or at least like a life-hack; sort of a “here’s what ya’ do when things get a little crazy.” Laura and I have always felt that if things get a little crazy, you shouldn’t be doing what you’re doing, or be in a place where you’re not supposed to be.
As much as we try to adhere to this advice, we are constantly reminded that the weather can turn on a dime in the Pacific Northwest, and things can get ugly fast, even if they started out nice and easy. The real challenge lies in knowing what to do when this happens, starting with sail areas.
While it is obvious that reefing the main reduces its surface area, and thus, the impact of power and drag from the wind — I wasn’t clear on exactly how much reduction occurred until I did a few calculations based on one of the geometry lessons that I presented in my high school math classes, by starting with some known quantities.
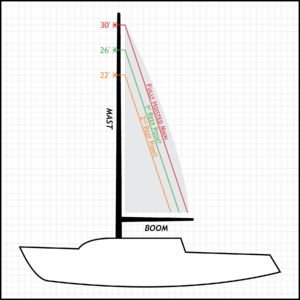
Ariel’s mainsail is about 30 feet tall, with the first reef point lowering it to about 26 feet, and the second one to about 22 feet. I wondered what percentage of the sail is exposed at each of the two points.
I could find the area of the fully hoisted main, and the resulting areas of the reefed sail, but mathematics is all about creating a theorem to generalize findings for any value. The concept that I utilized deals with comparing the areas of similar shapes, that is, figures that have the same ratios of length to width — in layman’s terms, shapes that result from being reduced or enlarged on a copy machine.
To illustrate the concept, consider what happens to a simple shape, like a square, when its dimensions are changed. Starting with a 10-inch by 10-inch square, imagine what happens to its area when its lengths are reduced to a 7 by 7 square or to 70% of its original lengths. The large square has an area of 100 square inches. The 70% square has an area of only 49 square inches (7 times 7), which is a little less than half of the starting value, an ostensible paradox, but also a proven theorem.
The theorem that supports this result says that the change in area between two similar shapes, like the full-sized main compared to its corresponding reefed form, is found by multiplying the percent change not just once, but twice (known mathematically as “squaring” the quantity), required because both the length and width have changed. For the example dealing with the square, the new area was 0.70 times 0.70, times the original area.
The effect on areas of shrinking or enlarging shapes is an often overlooked and misunderstood concept. In all of the years that I presented the idea in my classes, I felt that I was rarely able to solidify the relationship for my students. I think that our brains are hard-wired for linear, or one dimensional, thinking more easily than two or three dimensions.
So it’s easy to see that Ariel’s first reef point is about 87% of the original height (26 divided by 30). And as the second lowers it another 4 feet or so, the resulting height is about 73% of the full height (22 divided by 30). But the associated areas, crucial for reducing the wind pressure on the sail, are not so easy to conceptualize.
Nevertheless, I couldn’t prevent my teaching brain from kicking into gear to determine just how much of the mainsail is exposed at each of the two reef points. I realize, of course, that in the scheme of a pleasant day on the water, it’s not really numbers and calculations that matter, unless you’re talking heeling angle. And even then, it’s not really degrees of tilt; it’s degrees of relative comfort.
Allowing my exploration of the similar figure geometry theorem, I can conclude that the ratio of the area of the fully hoisted main to its size at the first reef point is 87% of 87%. That is, the reduced size is 0.87 times 0.87 of the full size, since the length of the sail at the boom is also reduced by an equal ratio (though not necessarily an equal length).
The resulting answer, 0.75, means that only 75% of the sail’s original, fully-hoisted area is experiencing wind pressure at the first reef point, a substantial change for only a four foot drop, and one that can reduce the heel and instability of Ariel to something manageable.
For the second reef point, at 73% of the height for the eight foot drop, the new area would be 0.73 times 0.73 times the full sail area, or about 0.53. So the second reef point produces a sail that is only 53% of the fully hoisted main! No wonder reefing is an effective method to utilize in high winds.
The beauty of mathematical formulas is often a double edged sword. While theoretical formulas provide a way to model the real world, they often oversimplify results and require empirical observations and experimentation to “force” them into compliance with practicality. Sail sizes (especially jibs and genoas) are usually not proportional. (For example, Ariel’s genoa possesses the same forestay height as the jib, but its foot is 1.5 times longer. The geometric theorem then, does not apply.) Even the roach of a mainsail will render the results of the calculation inaccurate. But even if producing an approximation, mathematical formulas can shed some light on lots of life, including boating procedures and specifically in reefing the main.
As I learn to sail Ariel, my background as a math teacher allows me to view some of the events and scenarios through a fascinating, but perhaps oversimplified lens. Although I must admit that when we are in the midst of a sailing application under stressful conditions, I never have the temerity to mention the mathematics of the occasion. At this point in our sailing lives, how to enjoy a relaxing day on the water is the only calculation or formula that I really care about.
David Casey is a retired math teacher and semi-professional woodworker and bass player. He plans on using his retirement to build a small sailboat and a kayak, and to explore the waters of southern Puget Sound.
Title photo by Ken Douglas.